Pravdepodobná podoba pravdy
Asi každý z nás sa už ocitol v situácii, keď naozaj potreboval hodiť kockou šestku. Niekto kocku pofúka, niekto požiada vyššie mocnosti, niekto uverí schopnostiam vlastnej ruky, a niekto hodí kocku mimo a víťazoslávne zvolá “Šestka!” dúfajúc, že mu to prejde. Všetci vieme, že hod kockou je dielom náhody …
Vďaka fyzike vieme, že ak za minútu spravíme 80 krokov, tak za 8 minút sa dostaneme do obchodu vzdialeného 640 krokov. Vieme si to spočítať. Rovnako vieme spočítať, kam dopadne raketa, ktorú vystrelíme. Keď hodíme kockou, tiež vieme spočítať výsledok. Platí to aj naopak. Ak chceme byť v obchode o 7 minút, vieme si spočítať, ako rýchlo musíme kráčať. Buď zvýšime počet krokov za minútu, predĺžime krok, alebo niečo medzitým. Ak chceme hodiť šestku, tak možností, ako to dosiahnuť, je ešte oveľa viac. V čom je teda problém, a prečo hovoríme pri hode kockou o náhode?
Hody bez náhod
Aby sme niečo vedeli vypočítať, potrebujeme do výpočtu doplniť vstupné hodnoty. Pri určení času, za ktorý prídeme do obchodu, sú týmito hodnotami dĺžka cesty, dĺžka kroku a frekvencia krokov. Ak sme trochu nepresní pri ich určení, tak čas, kedy prídeme do obchodu sa veľmi nelíši. Pri hode kockou je však situácia iná. Aj malá zmena v nastavení hodnôt počiatočných parametrov postačuje na to, aby sa výsledná hodnota výrazne zmenila. Hádzanie kockou sa preto javí ako náhodný proces. Čím vzdialenejšej budúcnosti sa naše predpovede týkajú, tým viac sa líšia, aj keď rozdiel počiatočných podmienok je zanedbateľný. Túto vlastnosť má okrem iného aj predpovedanie počasia či systémy troch telies (napr. Slnko, Zem a Mesiac).
Náhoda, o ktorej hovoríme v klasickej fyzike, vyjadruje našu praktickú neschopnosť určiť a kontrolovať všetky potrebné parametre týchto systémov. Napriek tomu však tieto systémy a ani ich správanie náhodné nie sú. Pri konkrétnom hode kockou padne šestka preto, lebo sme ju tak hodili. Nevieme však hodiť šestku cielene. Našu ruku neovládame dostatočne presne, kocka tiež nie je ideálna a povrch je pod mikroskopom pomerne členitý. Citlivosť výsledku na nepresnosti počiatočných nastavení ovplyvňuje predpovedateľnosť výsledku. Spôsobom hodu však môžeme zvýšiť šancu, že šestka padne. Pravdepodobnosti môžu byť predpovedateľné.
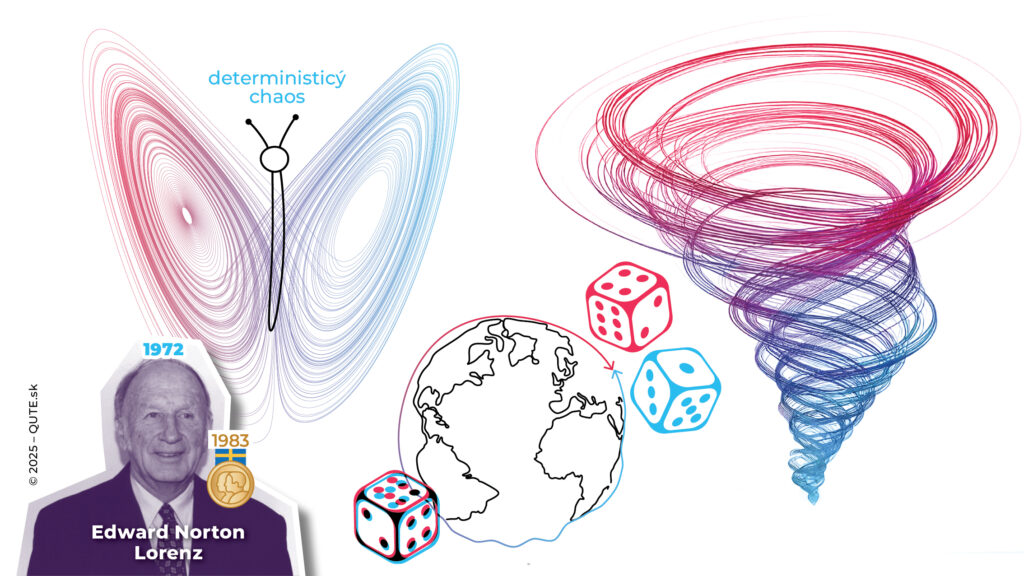
Motýlí efekt (Edward N. Lorenz, 1972) ilustruje na príklade počasia citlivosť vývoja systému na počiatočnom stave. Rozdiel zodpovedajúci mávnutiu motýlieho krídla v amazonskom pralese môže spôsobiť kdekoľvek na Zemi tornádo namiesto sucha. Znázornené motýlie krídla sú tzv. podivným atraktorom – objektom, ktorý vzniká pri študovaní deterministického chaosu.
Kvantum náhody
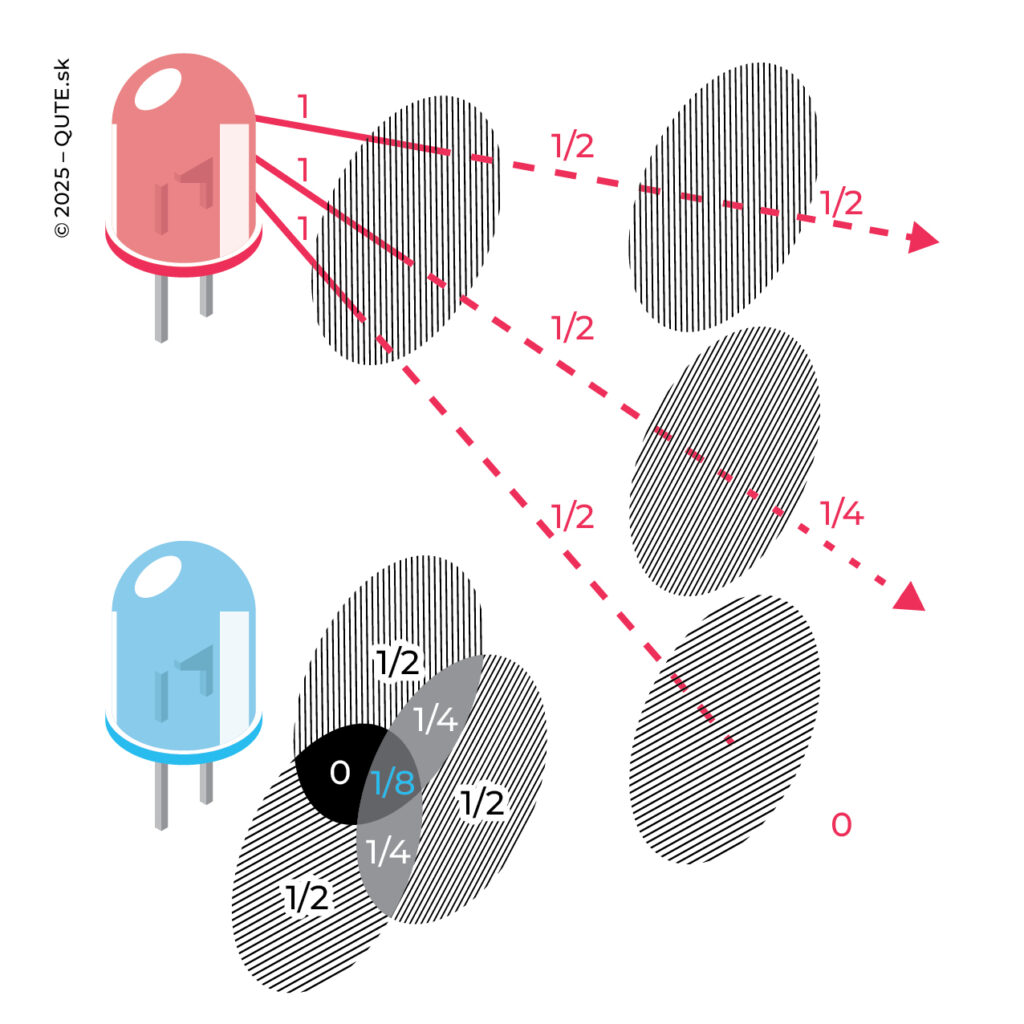
Svetlo má vlastnosť, na ktorú naše oko nie je vôbec citlivé – polarizáciu. Vieme o nej napríklad vďaka islandskému kalcitu – bájnemu slnečnému kameňu Vikingov. Pri správnom opracovaní funguje ako polarizačný filter – zariadenie, ktoré prepustí iba svetlo určitej polarizácie. Bežné zdroje svetla nie sú polarizované, a preto polarizačný filter zníži intenzitu svetla (počet fotónov) na zhruba polovicu. Pridanie ďalšieho rovnakého polarizačného filtra túto intenzitu už viac nezníži. Prečo? Pretože po prechode prvým polarizátorom je svetlo už „správne“ polarizované a druhý polarizátor tak nemá čo odfiltrovať. Záhada ukrytá v polarizácii sa prejaví, ak druhým polarizátorom pootočíme (okolo osi šírenia sa svetla). Intenzita svetla, ktoré prejde druhým polarizátorom, závisí od uhla pootočenia α a pri α = 90° svetlo úplne zmizne. Množstvo svetla, ktoré polarizátor odfiltruje, závisí od jeho natočenia.
Ťažšie otázky vystanú vtedy, keď si uvedomíme, že svetlo je zložené z fotónov. Polarizácia charakterizuje spôsob, akým šíriace sa svetlo okolo seba vyvoláva oscilácie elektrických a magnetických síl. Na úrovni fotónov je polarizácia vlastnosťou fotónu, ktorú fotón dokáže zmeniť. Napríklad pri prechode polarizátorom. Ako však vysvetlíme zníženie intenzity? Predstava, že prejde iba časť fotónu nie je správna, pretože by znamenala zmenu energie fotónu. To by znamenalo aj zmenu frekvencie. Nič také nepozorujeme, a jednoducho platí, že polarizátor niektoré fotóny pustí a niektoré nie. Ak je uhol medzi prvým a druhým polarizátorom α = 45°, tak polovica fotónov, ktoré prešli prvým polarizátorom, prejde aj druhým a polovica neprejde. Čo rozhoduje o tom, ktorý fotón prejde, a ktorý neprejde? Nevieme.
Záhady náhody
Ani kvantová fyzika nepozná spôsob ako vypočítať, či konkrétny fotón prejde, alebo nie. Tento proces považujeme za akt čistej náhody. Náhody, ktorá nie je dôsledkom neschopnosti niečo presnejšie nastaviť, alebo niečo presnejšie zmerať, ako pri hádzaní kockou. V tomto prípade musíme skonštatovať, že prechod fotónu cez polarizátor je principiálne náhodný. Vďaka kvantovej fyzike však dokážeme správne predpovedať pravdepodobnosti toho, či konkrétny fotón prejde, alebo neprejde. Nie hodnota prechodu, ale pravdepodobnosť prechodu je to, čo vieme presne vypočítať.
Nie je ľahké to prijať, ale náhoda je tou najkľúčovejšou vlastnosťou kvantovej fyziky. V známom výroku „Boh nehrá v kocky“ Albert Einstein vyjadril svoju skepsu voči kvantovej náhodnosti. Tento pocit nie je ojedinelý. Naše možnosti vystihuje citát iného velikána „Môžeme sa o tom hádať, môžeme s tým nesúhlasiť, ale to je tak asi všetko, čo s tým môžeme robiť.“ Náhoda má v kvantovom svete svoje pevné miesto. Pravidlo na výpočet pravdepodobností hodnôt akéhokoľvek kvantového parametra nesie meno nemeckého fyzika Maxa Borna, s ktorým sa (nielen kvôli menu) spája zrod kvantovej fyziky. Tento rok vyhlásilo OSN za Medzinárodný rok kvantovej vedy a technológií práve na počesť dvoch článkov z roku 1925, v ktorých Max Born a jeho študenti, Pascual Jordan a Werner Heisenberg, sformulovali prvú ucelenú teóriu mikrosveta – (maticovú) kvantovú mechaniku.
Pravdepodobnosť sa týka úplne každého parametra kvantového systému – nielen prechodu cez polarizátor, ale aj polohy elektrónu v atóme, alebo času rozpadu jadra v jadrovej elektrárni. Neznamená to však, že kvantové systémy sa správajú nepredvídateľne. Kvantový svet v pozadí má svoje jasné deterministické pravidlá. Schrödingerova rovnica, ktorá popisuje časové zmeny kvantových systémov, neobsahuje v sebe nič náhodné. Náhodné sú „iba“ výsledky našich konkrétnych pozorovaní, pričom ich pravdepodobnosti má kvantová fyzika úplne kontrolou a dokáže ich úspešne predpovedať a experimentálne overovať.
Pri pozorovaní kvantových systémov prichádza ku skokovej zmene ich vlastností. Každý fotón, ktorý prejde tým istým polarizátorom, má tú istú hodnotu polarizácie. Táto zmena nie je dôsledkom Schrödingerovej rovnice a nie je deterministická. Od vzniku kvantovej fyziky je náhodnosť, ktorá sa objavuje pri meraní, predmetom mnohých diskusií. Jej tajomstvo sa zatiaľ nepodarilo odhaliť a nie je vôbec jasné, že nejaké tajomstvo ukrýva.
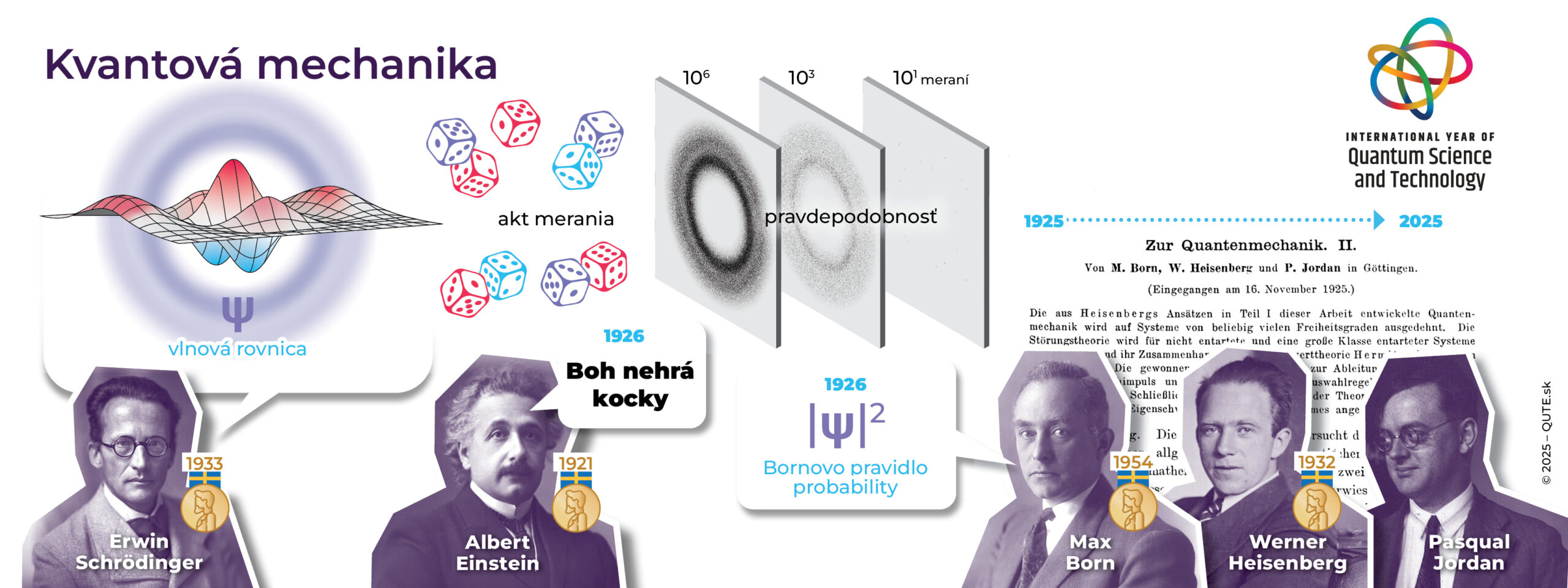
Bornovo pravidlo (Max Born, 1926) nám hovorí ako sa pozorované kvantové pravdepodobnosti (napravo) získajú z deterministického kvantovo-mechanického popisu kvantového systému (naľavo). www.quantum2025.org
Výhody náhody
Na prvý pohľad to tak možno nevyzerá, ale náhodnosť je rovnako užitočná ako istota. Umelá inteligencia, simulačné a optimalizačné algoritmy využívajú zdroje náhodných čísiel, aby sa efektívnejšie dopracovali k výsledkom. Pre bezpečnosť šifrovacích kľúčov je kľúčová rovnomerná náhodnosť, t.j. hodnoty nula a jedna vygenerované s rovnakou pravdepodobnosťou. Procesory samotné skutočnú náhodu generovať nedokážu. Používame špeciálne zariadenia – generátory náhodných čísiel (RNG).
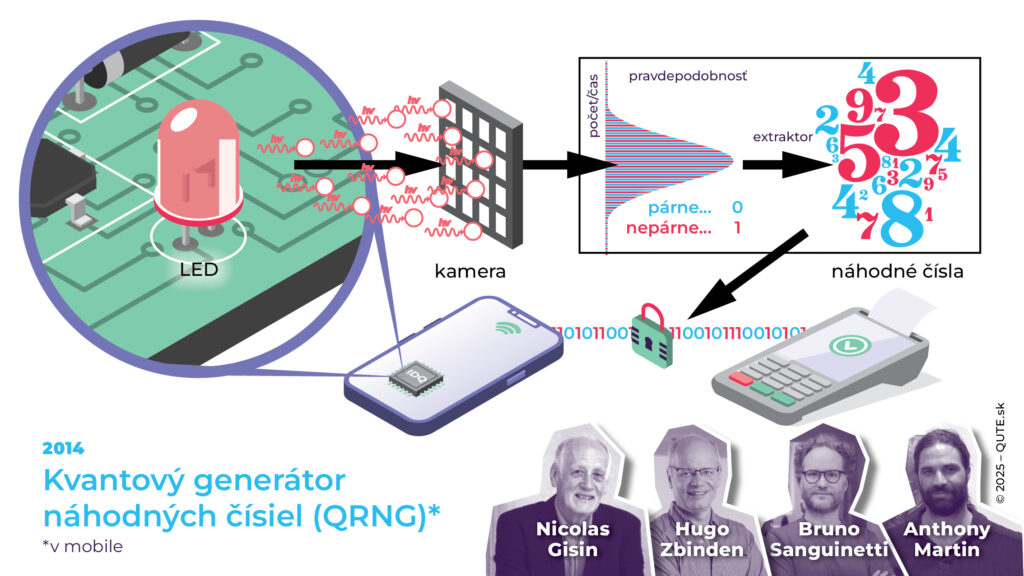
Kvantový generátor náhodných čísel. Obrázok zjednodušene zobrazuje fyzikálny princíp QRNG čipu Quantis (veľkosti 2,5 x 2,5 x 0,84 mm) umiestneného v mobile. Kamera zaznamenáva počty fotónov, ktorých pravdepodobnosti sú dané Poissonovou distribúciou. Pre párny počet priradíme hodnotu 0 a pre nepárny hodnotu 1. Takto získané hodnoty majú prakticky rovnakú pravdepodobnosť. Aby sme zistili rozdiel, tak by sme museli použiť toto zariadenie 10118-krát. (úprava: QUTE.sk)
RNG sú nenápadnou, ale veľmi dôležitou a rozšírenou technológiou. A kvantové systémy s náhodnosťou v “génoch” sú na konštrukciu takýchto zariadení ideálne. Či už ide o fotóny na polarizátore, alebo rádioaktivitu. Certifikované kvantové generátory náhodných čísiel (QRNG) si dnes môžeme kúpiť, zapojiť a používať. Na trhu nájdeme aj mobil so zabudovaným QRNG, ktorý pri generovaní náhodných bitov (niekoľko gigabitov za sekundu) používa kvantovú náhodnosť v počte vyžiarených fotónov z fotodiódy. Náhoda, ktorá dodáva istotu našim dátam a komunikácii.
Autor článku: Mário Ziman, Fyzikálny ústav SAV, v.v.i. v Bratislave
Ilustrácie: Diana Cencer Garafová, QUTE.sk – Národné centrum pre kvantové technológie
Zdroje obrázkov: wikipedia public domain


