Qubit
Vedci sa začali zaoberať skúmaním sveta na jeho najmenšej možnej úrovni, v mierke atómov a elementárnych častíc, už pred viac ako storočím. Zistili, že v tomto „mikrosvete“ prestávajú platiť klasické fyzikálne predstavy o tom, ako by sa čo malo správať, a nastupujú zvláštne, neintuitívne pravidlá, ktoré dnes poznáme ako kvantovú mechaniku.
Dlho sme dokázali kvantové zákony iba opisovať a teoreticky vysvetľovať. Skutočný prelom priniesol až rozvoj technológií a experimentálnych metód, ako napríklad vznik iónovej pasce v roku 1995, ktoré nám prvýkrát umožnili aktívne zasahovať do kvantových stavov a manipulovať s nimi. Toto obdobie, v ktorom kvantové javy začíname využívať vo svoj prospech, označujeme ako druhú kvantovú revolúciu.
Práve schopnosť cielene ovplyvňovať kvantové stavy umožnila vznik elementárnej jednotky kvantovej informácie – kvantového bitu, teda qubitu. Qubity sa stali základom kvantového počítania v kvantových počítačoch, ktoré vďaka nim dokáže spracovávať informácie spôsobom, aký je pre klasické počítače nedosiahnuteľný.
“Príroda predsa nie je klasická a ak chcete vytvoriť simuláciu prírody, tak ju radšej urobte kvantovo-mechanickú – a, veru, je to nádherný problém, pretože to vôbec nevyzerá jednoducho.”
— Richard P. Feynman, prednáška „Simulating Physics with Computers“, MIT Physics of Computation Conference, máj 1981 (uvedená v International Journal of Theoretical Physics, 1982)
Kvantové vlastnosti qubitu
Zatiaľ čo klasický bit predstavuje základnú jednotkou informácie a môže nadobudnúť len jednu z dvoch hodnôt, buď 1 alebo 0, Qubit je úplne odlišný. V kvantovom svete má totiž schopnosť nachádzať sa v stave superpozície, čo znamená, že môže byť v stave 0 aj 1 zároveň, a to aj v rôznych pomeroch. Qubit v superpozícii zostáva až dovtedy, kým ho nezmeriame. Vtedy už ako výsledok dostaneme buď 0 alebo 1.
Pravdepodobnosť, že po meraní dostaneme 0 alebo 1, je určená tzv. amplitúdou pravdepodobnosti. Môžeme si ju predstaviť ako vlnu, ktorá určuje pravdepodobnosť merania určitého výsledku. Vlny majú schopnosť navzájom sa posilniť alebo oslabiť nazývanú interferencia. Interferencia sa pri kvantovom počítaní využíva na zosilnenie pravdepodobnosti merania správnych výsledkov a potlačenie pravdepodobnosti merania tých nesprávnych.
Ďalším kľúčovým princípom kvantového počítania je previazanie qubitov (po anglicky „entanglement“). Ak sa dva alebo viac qubitov previaže, prestávajú existovať ako samostatné jednotky a vytvoria spoločný kvantový stav. Znamená to, že zistenie stavu jedného qubitu okamžite prináša informáciu aj o druhom bez ohľadu na ich vzdialenosť. Previazanie umožňuje, aby qubity pracovali ako jeden koordinovaný celok a spracovávali informácie spôsobom, ktorý klasické výpočtové systémy neumožňujú.
Znamená to, že zistenie stavu jedného qubitu okamžite prináša informáciu aj o druhom bez ohľadu na vzdialenosť. Previazanie umožňuje, aby qubity pracovali ako jeden koordinovaný celok a spracovávali informácie spôsobom, ktorý klasické výpočtové systémy neumožňujú.
Blochova sféra
Na geometrické zobrazenie jedného qubitu sa používa Blochova sféra. Qubity sa na nej zobrazujú ako body na jednotkovej guli (takej, ktorej polomer je rovný 1 grafickej jednotke). Blochova sféra nie je fyzické zobrazenie qubitu v priestore, ale veľmi užitočná vizuálno-matematická pomôcka, ktorá umožňuje intuitívne pochopiť jeho kvantové vlastnosti.
Pravdepodobnosť, že po meraní dostaneme 0 alebo 1, je určená tzv. amplitúdou pravdepodobnosti. Môžeme si ju predstaviť ako vlnu, ktorá určuje pravdepodobnosť merania určitého výsledku. Vlny majú schopnosť sa navzájom zosilniť alebo oslabiť nazývanú interferencia. Interferencia sa pri kvantovom počítaní využíva na zosilnenie pravdepodobnosti merania správnych výsledkov a potlačenie pravdepodobnosti merania tých nesprávnych.
Ďalším kľúčovým princípom kvantového počítania je previazanie qubitov (po anglicky „entanglement“). Ak sa dva alebo viac qubitov previaže, prestávajú existovať ako samostatné jednotky a vytvoria spoločný kvantový stav.
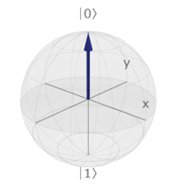
Aby sme si to vedeli lepšie priblížiť, môžeme si Blochovu sféru predstaviť ako zemeguľu (avšak nie úplne ako geoid, ale ako perfektnú guľu). Qubit sa môže nachádzať hocikde na tejto zemeguli, toto nám umožňuje do qubitu zakódovať nekonečne veľa rôznych možných stavov. Stav 0 je reprezentovaný na severnom póle tejto zemegule a stav 1 na jej južnom póle. Ak sa však posunieme mimo pólov, stav qubitu už bude v superpozícii.
Čím bližšie je stav qubitu k jednému z pólov, tým väčšia je pravdepodobnosť, že po meraní dostaneme práve stav zodpovedajúci tomuto pólu. Na rovníku by sme sa nachádzali v rovnomernej superpozícii 0 a 1, čiže máme rovnakú šancu, že dostaneme 0 alebo 1. Ale čo ak sa prechádzame po rovníku alebo iných po iných zemepisných šírkach? V takom prípade meníme tzv. fázu qubitu, teda relatívne natočenie medzi stavmi 0 a 1, ktoré síce nemení pravdepodobnosti merania, ale zásadne ovplyvňuje výsledok merania, keď qubit necháme interferovať s inými qubitmi alebo naň pôsobíme hradlami.
Kvantové hradlá predstavujú operácie, ktoré môžeme s qubitmi robiť. Inak povedané, dokážeme nimi na qubity pôsobiť a meniť ich stav. Spájaním hradiel do postupností vytvárame kvantové algoritmy, ktoré tvoria základ kvantového počítania.
Základné kvantové hradlá:
1. Hadamardovo hradlo: pripraví qubit do superpozície
2. Pauliho X hradlo: prevráti stav qubitu na opačnú stranu Blochovej sféry
3. CNOT: pracuje s dvomi qubitmi a mení stav druhého qubitu len vtedy, ak je prvý v stave 1, čím sa vytvára základná forma kvantového previazania
Okrem týchto základných kvantových hradiel existuje ešte mnoho ďalších, ktoré umožňujú ďalšie zložitejšie operácie. Zaujímavé však je, že v kvantovom počítaní neexistuje hradlo, ktoré by vedelo skopírovať qubit. Táto skutočnosť sa nazýva no-cloning theorem a patrí medzi základné pravidlá kvantovej mechaniky. Dôvod je ten, že qubit môže byť v superpozícii, a taký stav nevieme úplne presne opísať bez toho, aby sme ho zmerali. Ak ho zmeriame, dostaneme už len konkrétny výsledok (0 alebo 1) a stratíme tak všetku informáciu o superpozícii..
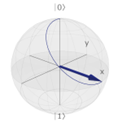
1, Hadamardovo hradlo
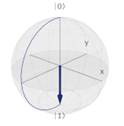
2, Pauliho X hradlo
Kvantové počítanie
V dnešnej dobe už začínajú prvé praktické testovania kvantových počítačov. Zatiaľ ide najmä o overovanie možností tejto technológie, aj keď jednoduché programy si môžu vyskúšať už aj bežní užívatelia. V praxi poznáme rôzne druhy kvantových počítačov, pričom každý z nich využíva iný typ qubitov.
Na vytvorenie qubitu potrebujeme dva navzájom sa vylučujúce stavy, ktoré ale dokážu spolu existovať v superpozícii. Môže ísť o polarizáciu svetla, energetické hladiny v atóme alebo dokonca o spin elektrónu či prúd v supravodivom obvode.
Kvantové počítače však stále čelia viacerým technickým obmedzeniam. Ich fungovanie komplikuje šum a strata informácií, čo vedie k častým chybám. Aj keby sa v budúcnosti vedcom podarilo tieto problémy odstrániť, kvantové počítače nemožno vnímať ako náhradu klasických počítačov. Predstavujú skôr mimoriadne užitočný nástroj určený na riešenie veľmi špecifických úloh. Medzi ne patrí napríklad vývoj nových liekov a materiálov, optimalizácia dopravy, logistiky či finančných systémov. Významnú úlohu zohrávajú aj v oblasti šifrovania a kybernetickej bezpečnosti.
Druhy qubitov
Najbežnejším druhom kvantového počítača je ten, ktorý používa supravodivé qubity. Využíva supravodivé obvody a schopnosť tunelovania elektrónov. Operuje pri extrémne nízkych teplotách, aby sa zabránilo šumu z tepelných vibrácií. Na dosiahnutie týchto teplôt sa využíva špeciálny, a často veľmi drahý, chladiaci systém, ktorý tvorí väčšinu počítača. Manipuluje s qubitmi pomocou mikrovlnných pulzov a elektromagnetických polí. Výhodou tejto technológie je rýchlosť operácií, dobrá kompatibilita s klasickou elektronikou a možnosť zostrojiť počítače s veľkým počtom qubitov. Nevýhodou však je, že qubit dokáže udržať svoj kvantový stav iba veľmi krátko a už spomínané chladenie takmer na absolútnu nulu.
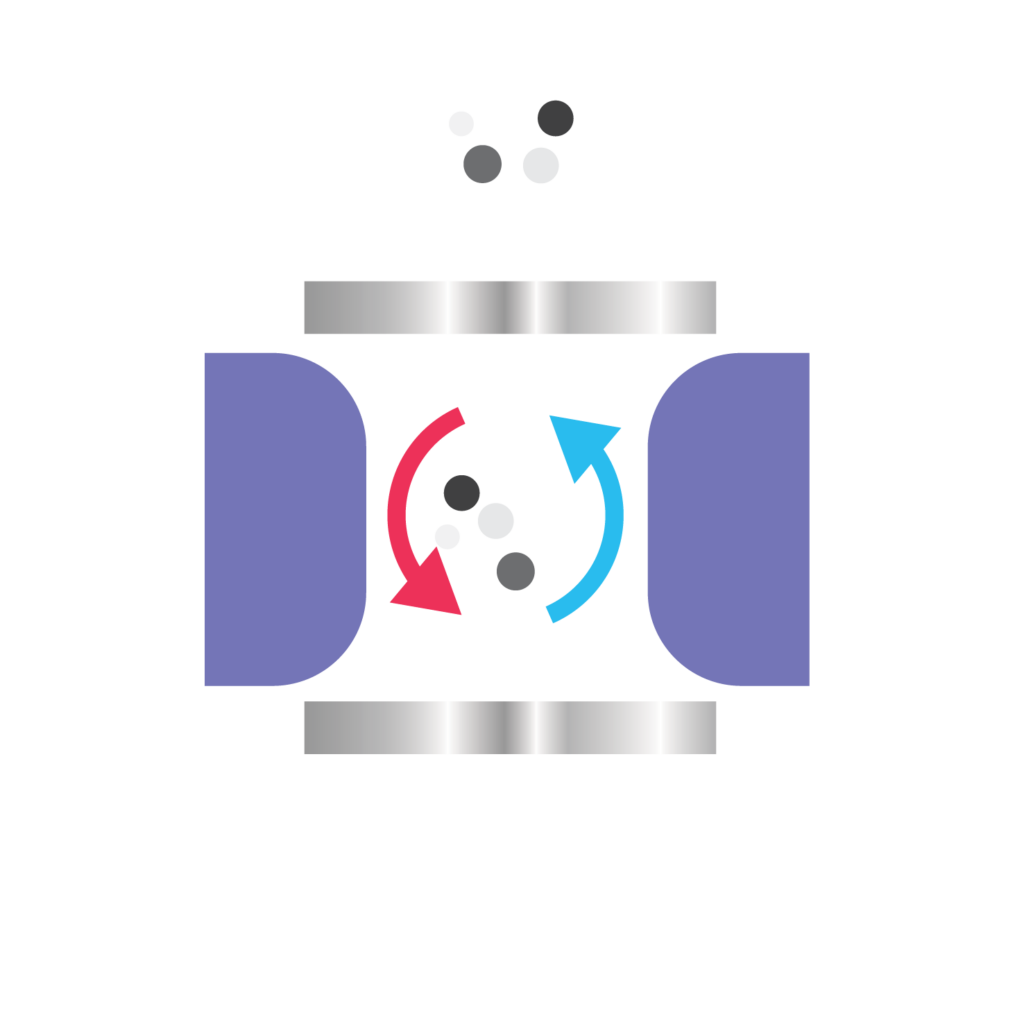
Ďalší veľmi sľubný druh kvantového počítača využíva iónové qubity. Ióny sú uväznené v tzv. elektromagnetických pasciach pomocou elektrického prúdu a sú manipulované veľmi presnými laserovými impulzami. Dva stavy zodpovedajú základnej a excitovanej energetickej hladine. Operácie sú síce pomalšie a vytvorenie počítača s väčším počtom takýchto qubitov je náročnejšie než pri supravodivých kvantových počítačoch, no vynikajú vysokou stabilitou a presnosťou.
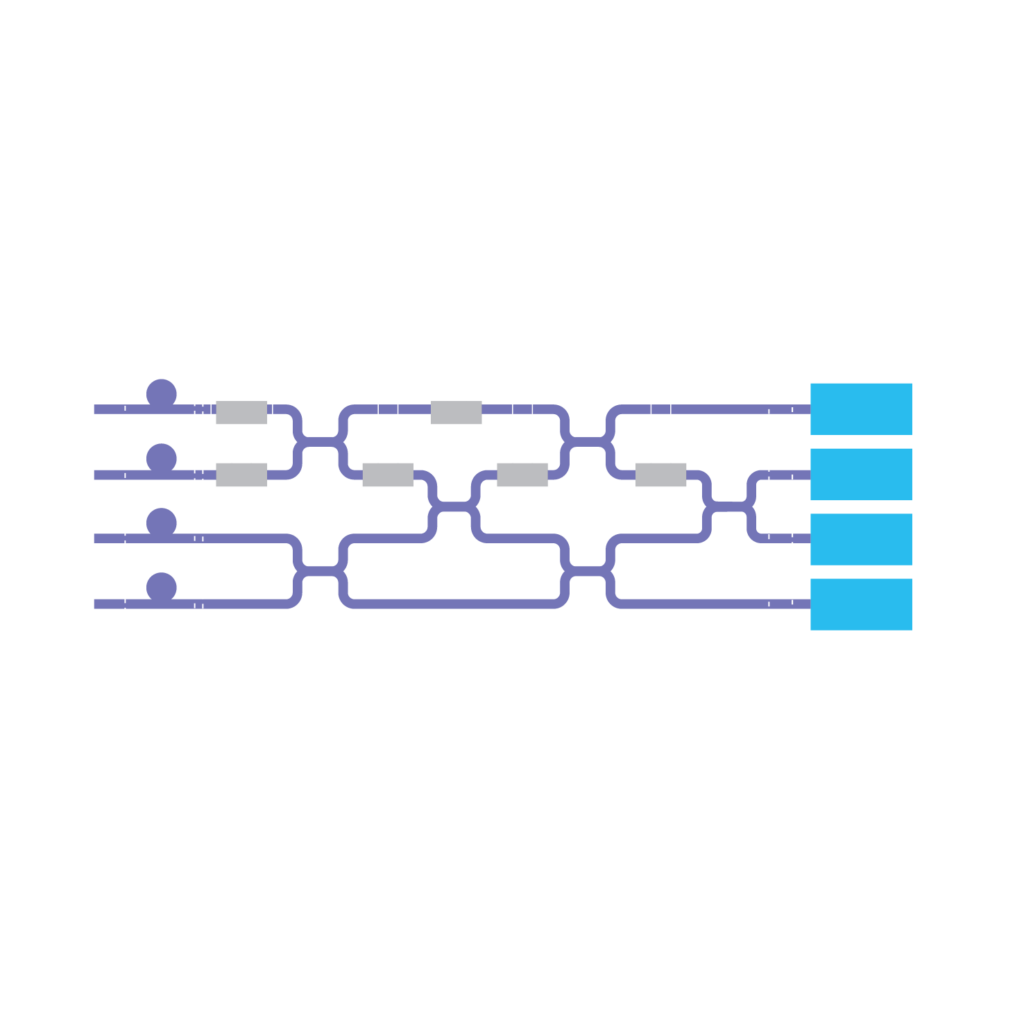
Okrem supravodivých a iónových qubitov existujú aj iné prístupy. Fotónové qubity využívajú svetlo, teda jednotlivé fotóny, spinové qubity pracujú so spinom elektrónu alebo jadra atómu.
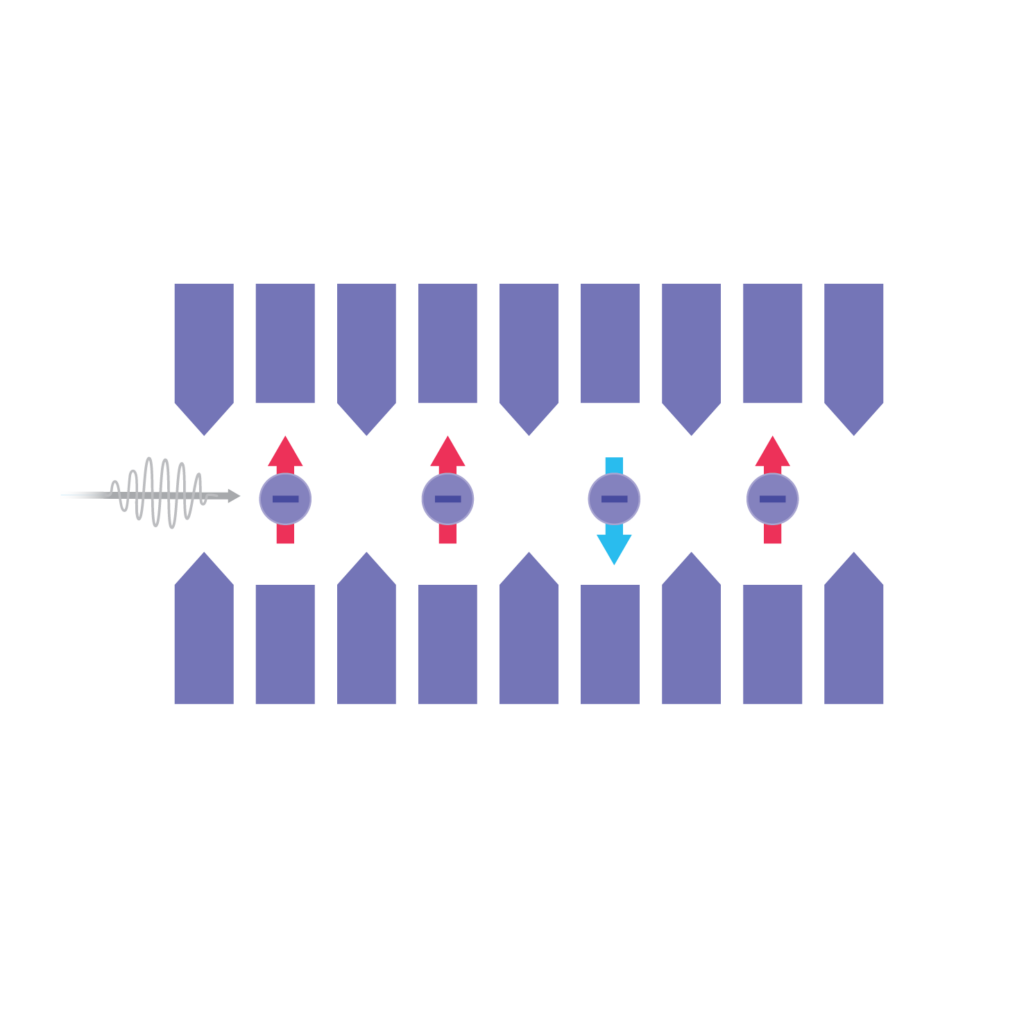
Topologické qubity sú zatiaľ prevažne teoretické, no ponúkajú potenciál vysokej stability voči chybám, čo je jedna z najväčších výziev kvantového počítania.
Algoritmy
Za väčšinu spomínaných praktických využití kvantových počítačov vďačíme najmä dvom kvantovým algoritmom, Shorovmu a Groverovmu.
Shorov algoritmus patrí medzi najznámejšie kvantové algoritmy a už od svojho predstavenia v roku 1994 vzbudzuje veľkú pozornosť. Jeho autor, matematik Peter Shor, totiž ukázal, že vďaka nemu je možné rozkladať veľké čísla na prvočísla neporovnateľne rýchlejšie, ako by to dokázali klasické počítače. Práve na matematickú zložitosť tohto rozkladania, faktorizáciu, sa totiž spoliehajú moderné spôsoby šifrovania správ a pomocou Shorovho algoritmu je možné ich prelomiť podstatne rýchlejšie. Zatiaľ ešte kvantové počítače nie sú dostatočne výkonné na to, aby predstavovali reálnu hrozbu pre bezpečnosť našej komunikácie, no napriek tomu sa odborníci už dnes aktívne venujú vývoju tzv. kvantovej a postkvantovej kryptografie, ktoré budú voči takýmto útokom odolné.

Groverov algoritmus predstavil indický informatik Lov Grover v roku 1996. Jeho cieľom je zrýchliť vyhľadávanie v neusporiadaných dátach. Tento algoritmus zrýchľuje hľadanie správnej odpovede z obrovského zoznamu položiek. Zatiaľ čo klasický počítač musí prechádzať položku po položke, kvantový vie pomocou interferencie zosilniť pravdepodobnosť, že si vytiahneme práve hľadanú položku. Groverov algoritmus sa dá využiť pri vyhľadávaní v databázach, riešení optimalizačných problémov, v strojovom učení či v chemických simuláciách. Podobne ako Shorov algoritmus sa dá tiež uplatniť aj v kryptografii. Ak je dnes šifra bezpečná napríklad pri 2¹²⁸ možných kľúčoch, s kvantovým počítačom a Groverovým algoritmom by stačilo približne 2⁶⁴ krokov, čo je už výrazne menej, ako keby sme kľúče skúšali jeden po druhom. Aj preto sa pri navrhovaní nových kryptografických protokolov zohľadňuje nielen Shorov, ale aj Groverov algoritmus.


zdroj : Wikipedia
Fun fact zo zvieracej ríše
Niektoré sťahovavé vtáky, napríklad červienky obyčajné (lat. Erithacus rubecula), dokážu preletieť tisíce kilometrov a vždy nájdu cestu späť domov. Vedci sa domnievajú, že ich mimoriadny orientačný zmysel sa dá pripísať javom kvantovej mechaniky. V očiach vtákov sa nachádza špeciálny proteín, v ktorom dopad svetla spôsobí uvoľnenie jedného elektrónu z elektrónového páru a jeho presun do inej časti tohto proteínu.
Tieto dva elektróny už nie sú nútené mať opačný spin, ako keď boli v spoločnej väzbe, a vstupujú do superpozície stavov: môžu mať rovnaký spin alebo opačné spiny. Magnetické pole Zeme jemne mení pravdepodobnosť výsledného stavu. Tieto výsledné stavy následne ovplyvňujú priebeh chemických reakcií v oku vtáka a vytvárajú prirodzený kompas s ohromnou presnosťou. , čo my nazývame qubit a snažíme sa udržať v laboratóriách kvantových počítačov, vtáky pravdepodobne využívajú každý rok počas migrácie. Kvantová mechanika tak vtákom pomáha prežiť a udržiavať si ich rytmus sťahovania.


